Impedance of Wilkinson microstrip divider

The Wilkinson divider is a device designed to divide the power of a microwave signal into two output ports. Different sections of the divider consist of a microstrip line of different widths. There are four such sections in total and each has its own impedance.

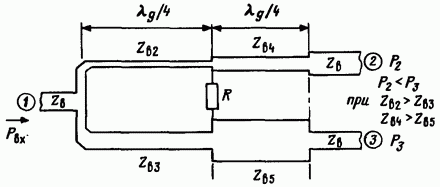
first_impedance

electrical_impedance of the first section.

Symbol:

Z_1

Latex:

\(Z_{1}\)

Dimension:

impedance

second_impedance

electrical_impedance of the second section.

Symbol:

Z_2

Latex:

\(Z_{2}\)

Dimension:

impedance

third_impedance

electrical_impedance of the third section.

Symbol:

Z_3

Latex:

\(Z_{3}\)

Dimension:

impedance

fourth_impedance

electrical_impedance of the fourth section.

Symbol:

Z_4

Latex:

\(Z_{4}\)

Dimension:

impedance

transmission_line_impedance

electrical_impedance of the transmission line to which the divider is connected.

Symbol:

Z_0

Latex:

\(Z_{0}\)

Dimension:

impedance

power_ratio

Ratio of the power at the outputs of the divider.

Symbol:

k

Latex:

\(k\)

Dimension:

dimensionless

law

[Z_1, Z_2, Z_3, Z_4] = [Z_0 * sqrt(k * (1 + k^2)), Z_0 * sqrt((1 + k^2) / k^3), Z_0 * sqrt(k), Z_0 / sqrt(k)]

Latex:

\[\begin{split}\begin{pmatrix} Z_{1} \\ Z_{2} \\ Z_{3} \\ Z_{4} \end{pmatrix} = \begin{pmatrix} Z_{0} \sqrt{k \left(1 + k^{2}\right)} \\ Z_{0} \sqrt{\frac{1 + k^{2}}{k^{3}}} \\ Z_{0} \sqrt{k} \\ \frac{Z_{0}}{\sqrt{k}} \end{pmatrix}\end{split}\]